NAVALNY Alexei

 NAVALNY Alexei

04 Jun 1976 GREG    CAL
friday GREG
 | lat 56° 37' 0" | N 37°0' E
0
---------------------------------
natal (bt) 15 h 27 min
raas-rams :0h 1' 43"
reckoned bt Lat --> lmt 13 h 30 min
tu 10h 30' 24"
tsn 5h 49' 57"
---------------------------------
timezone  : 3 (-E)
DST : 0 (-)
Equation of time 0h 1' 43"
ΔT 0h 0' 46"
---------------------------------

Russian political activist, lawyer, anti-corruption activist, and political prisoner, claimed by The Wall Street Journal in 2012 as "the man Vladimir Putin fears most". Navalny's death in 2024 left Russia without an opposition leader.
In August 2020, Navalny was hospitalised in serious condition after being poisoned with a Novichok nerve agent. He was medically evacuated to Berlin and discharged a month later. Navalny accused Putin of being responsible for his poisoning, and an investigation implicated agents from the Federal Security Service. In January 2021, Navalny returned to Russia and was immediately detained on accusations of violating parole conditions while he was hospitalised in Germany which were imposed as a result of his 2014 conviction.
In December 2023, Navalny went missing from prison for almost three weeks and then re-emerged in an arctic circle corrective colony in the Yamalo-Nenets Autonomous Okrug. On 16 February 2024, the Russian prison service reported that Navalny had died at the age of 47.

THEME

SU is P with a [-11] score
MO is E with a [4] score
VE is T cb  with a [9] score
JU is te with a [0] score

MA is P with a [-11] score

SA is D with a [-4] score


we see below the list of  aspects :
---------------------------------------
        VE 0 SU Oc  MA 60 SU Or                                               MA 60 VE Or                    
---------------------------------------
SU is opp to Part of Fortune


The traditionnal almuten (Omar, Ibn Ezra) is SA
we see below the list of dignities for SA :
---------------------------------------
[ term 2 tri 2 rul 0 exn 0 fac 2 ]
[ su 1 mo 2 asc 0 syg 1 pof 0 ]
---------------------------------------
Note 1 : the ‘almuten figuris’ is the lord of the chart, but its determination obeys somewhat different rules according to the schools. The tradition is based above all on the zodiacal dignities. (see p,e,  Alcabitius, Introduction, 59-61, 117 and Avenezra, Nativites, 101) – almuten = al-mu’tazz (arabic term)
[7] As for the governor which is the <planet> predominating (al-mubtazz) over the birth from which one indicates the conditions of the native after the haylāğ and the kadhudāh,n it is the planet having the most leadership in the ascendant, the position<s> of the two luminaries, the position of the Lot of Fortune and the position of the degree of the conjunction or opposition which precedes the birth. When a planet has mastery over two, three or four positions by the abundance of its shares in them, it is the governor and the predominant <planet> (al-mubtazz) and the indicator after the haylāğ and the kadhudāh. From it one indicates the conditions of the native. Some people use it instead of the kadhudāh in giving life.  [Al-Qabisi , Charles Burnett, Keji Yamamoto, Michio Yano, The Introduction to Astrology, IV, 7, p, 117, Warburg, 2004]
Note 2 : There are at least 4 systems for determining the almuten depending on whether the combinations of triplicities and terms are used: the Ptolemaic almuten (followed by Lilly) with Ptolemaic terms ; the same with Egyptian terms; the almuten of Dorotheus with Ptolemaic terms ; the same with Egyptian terms, knowing that one can embellish the whole thing with different weighting system (like Lilly or not using weights like Montanus) [cf. Temperament: Astrology's Forgotten Key, p. 79, Dorian Gieseler Greenbaum 2005]

The Lilly (Ptolemaïc) almuten is MO

In our experience, it seems that Ptolemy's almuten allows one to first appreciate the static side of the natal chart and that the Lilly-type elaboration allows one to deepen the more ‘temporary’ or ‘dynamic ‘ relationships (cf, Shlomo Sela, Ibn Ezra, on Nativities and Continuous Horoscopy, appendix 6, quot 2  ; Horary astrology p, 458, Brill, 2014)
---------------------------------------

HYLEG – ALCHOCODEN – domification ,

We see that the nativity is diurnal (or nocturnal) and the moon is waxing (waning). This immediately makes it possible to orient the search for the hyleg towards SU or MO. We then seek the point which is both in Ptolemaic aspect and in dignity with the hyleg. This is the alchocoden. In the lower table, information is given on the alchocoden point (including dignity, power, retrograde, the house situation and especially the important fact of knowing if the alchocoden point is within 5° of the next cusp, in which case it must be removed (or added if he is retrograde) a certain number of degrees (life points).Finally, it may be necessary to add points depending on the place of JU and VE in relation to the upper meridian or the rising.

ZODIACAL – MUNDANE

In our research, we hypothesised that the mundane chart alone should be considered; also we must base on the aspects taken in the semi-arcs the research of the degrees likely to be considered in the duration of the life.
In the case of NAVALNY Alexei we have the table above which allows us to estimate the breakdown of aspects between the different planets and the alchocoden.
When considering a theme, the first thing is to observe whether it is diurnal or nocturnal. In the case of NAVALNY Alexei, it is .
In this case, the first point to check is SU. If  SU is well disposed, it can claim 1st stage to be HYLEG.

SU is P and therefore seems weak, with a dignity score of [-7],
Moreover, when we look for the dignities that appear in the zodiacal inscription of SU, we find at least one
we find at least one aspect to match with the dignities
We'll see later what we get when we search for mundane dignities.
So : the hyleg is SU as dignity is P and aspect is conjunction

Now we must look for the alchocoden: it is the planet which has the maximum dignity with regard to the hyleg and which exchanges a Ptolemaic aspect with the hyleg.
if we consider the ZODIACAL system, we observe a conjunction aspect of VE.
At the same time, it appears that VE has  dignity of TERM over ASC.
So we have two possibilities with our hypothesis : first choose SU for hyleg ; second choose the MUNDANE system and try to find another couple of hyleg/alchocoden,
If we choose now SU we must know that Dorotheus, Al Qabisi, and Ptolemy, agree with this choice
In case of SU is the Hyleg, there is then one candidate to be the alchocoden: VE
First, we have to see which candidate has the most dignity: here, VE has candidate alcho dignities referring to SU : [TERM]
First, VE is linked with SU by a [conjunction] aspect and a [TERM] dignity,
However, VE is [T cb] and has a power of [3], VE has a Kadkhudah score of [1]
VE is located at 70,18° at more than 5° from [Δ degrees cups sup [IX] : 18,2° (240)] and has a domitude regio of : [258,2] for a latitude of [-0,28°]
Now, we have to take account of the radix zodiacal aspects,
------------------------------------------------------
    MA 60 VE: -12,77  
------------------------------------------------------
Without any change, we find with VE as Kadhkhudah : Y = 45 as a result of VE CADENT years
But as VE is TERM, following William Lilly in Christian astrology, p, 115 (London, 1647) on his table of Fortitudes and debilities, we remove 1/5 of his value, as dignity for VE is     T cb   Occ  (ie 0)
------------------------------------------------------
So, zodiacal Y =31,48
------------------------------------------------------
MUNDANE
Now we have to think about the hyleg to find: MO is not suitable; the rule is then in a nocturnal theme to reconsider first the case of SU,
In the mundane theme with  domification, we find a TERM :VE with a conjunction for SU
VE is in term
So the standard Years are : 8
But, according to MONTULMO, if the  alchocoden (VE) is in IX house and has two dignities in this house ; so  IX is not is not considered as cadent but as succedent. It also appears more logical that house IX, adjoining the MC and hylegial, has a standard score at least equal to 2/3 of the succedent score.
So the actual Y is 45,
To do this, the procedure is not unequivocal but one of the most logical seems to me to be the one mentioned by Auger Ferrier in ‘Jugements astronomiques sur les nativités’, Rouen, 1583 (pp, 39-51 and notably pp, 43-48). Note that Auger Ferrier's comments appear directly related to those of Montulmo in his’ De Nativitatum liber praeclarisimus’ (Nuremberg, 1540), cap IV & VII. Book translated by Robert Hand (‘On the Judgment of Nativities’, part 1 & 2, Project Hindsight, vol X)
the years of life are identified for the [cad] and [ang] houses relative to the alchocoden.

cad= 45
ang= 82
we take the difference = -37
take the 1/5 of this difference = -7,4
then take the difference between 5 and the actual position of the point = 0 (11,8)
take the rule of three =
Then we add the ang Y 8 and  = 8
we must add [ domVE (258,2) - cusp (240) ] x [ cusp ang (45) - cusp succ 82) ]/5/5
So, we add to Y : Δ = 0
Now, we have to take account of the radix mundane aspects,
SU 0 VE: 1,24        minus alcho dy (0)
VE appears to be T cb and his power is 3
Given that VE is T cb, we need to remove nothing from Y =48,49 so : 0 Y
Y=   46,24
-----------------------------------------------------------------------------------------------------------------------
Here we find the number of points granted to the planets according to the aspects exchanged. There are 3 aspects in global:

VE 0 SU Oc: it amounts to VE 9.69 pts and to SU -0.79 pts so value of * =
MO 60 SU Or: it amounts to MO 4.52 pts and to SU -2.42 pts
JU 60 MA Oc: it returns to JU 0 pts and to MA 7.45 pts.
Either for SU -3.21, for MO 4.52, for VE 9.69.

This system of points is based on the one hand on the orb of the aspect in % and on the other hand on the method of Georges MUCHERY (Traité Pratique d'Astrologie Judiciaire, le Chariot, Paris, 1971, pp. 19- 20). In our opinion, it provides an interesting alternative to the astrodyne method (Elbert Benjamine (aka C.C. Zain) of the Church of Light in Los Angeles and W.M.A. Drake, "Course XVI, Stellar Healing" book and Elbert Benjamine's "The Astrodyne Manual " 1946). In particular, this system does not take into account the theme in mundo; it also does not take into account peregrine points.

A special point must be made regarding the sextile JU-MA because these two points are joined by a parallel. As I have mentioned many times, the // is a special connection between two significant points and it is in any case not an aspect. When it is engaged in an in mundo theme, in addition to the value of the points engaged, it is necessary to study the houses which host these points. Here, in Regiomontanus domification, it turns out that the two points are in conjunction with the cusps of houses IX and XI.
-----------------------------------------------------------------------------------------------------------------------

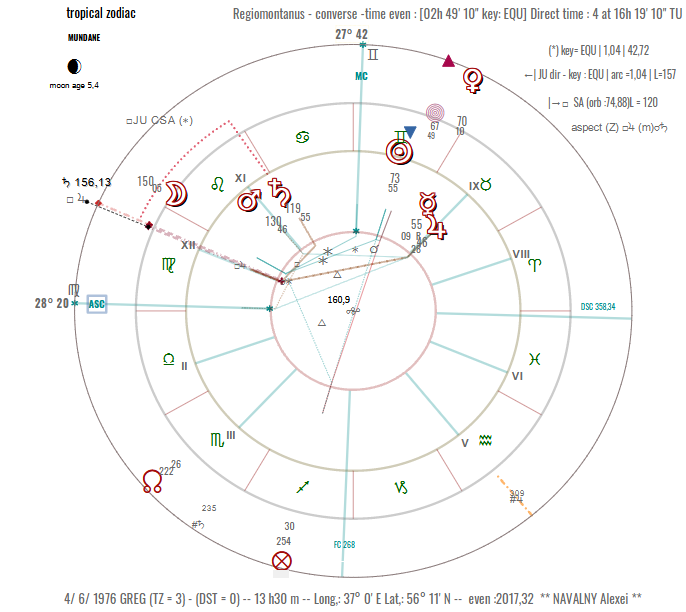
DIRECTIONS on 27 APRIL 2017

On 27 April 2017, Navalny was attacked by unknown assailants outside his office in the Anti-Corruption Foundation who sprayed brilliant green dye, possibly mixed with other components, into his face. He said he had lost 80 percent of the sight in his right eye. He also said that his doctor believed there was a second corrosive substance in the liquid and that "there is hope" the lost eyesight would be restored.

DIRECTIO CONVERSA (m) [c] ☌ ♄ ◻ ♃

speculum	Lat	Dec	AR	MD	SA	HA
SA	0,44 N	20,6 N	122,20	34,71 D	124,14 D	89,43 E
□JU	0 S	9,02 N	158,54	71,05 D	103,7 D	32,65 E

– MD = meridian distance (from MC if SA f [SA]  is diurnal or IC if Sa f  is nocturnal)
– SA = semi-arc (if f is diurnal, SA f [SA] is D and all MD’s and SA’s are D, otherwise N
– HA = horizontal distance (from the nearest horizon W or E for f [SA] and m □JU)
under bracket [] the fixed point, (here SA)
----------------------------------------------------------------------------------------------------------------------------

DP REGIOMONTANUS			DP REGIO-CAMPA C		DP REGIO-CAMPA D
	A2 □JU	A1 SA	A1 SA	A2 □JU	A2 □JU	A1 SA
Tan A	tan dec/cos dm		24,57		26,05
B (1)	+LG-A or -LG+A		31,61		30,13
Tan C	cot DM.cos B/cos A		53,51		-18,29
Sin pole (2)	Cos C.sin LG		29,61		52,07
Sin DA (3)	Tan pole A1.Tan Dec A2 Tan pole A2. Tan Dec A1	DAP	12,33	5,18	11,75	28,84
AO (4)	AR ± DA		109,87	153,36	146,78	93,36
arc	AO1 – AO2			-43,49		53,42
				CONVERS		DIRECT

----------------------------------------------------------------------------------------------------------------------------

(1) B must be < ε
(2) sign of pole has the same sens of LG for DA Here, DA = DA/pole A
(3) [+] sign if pole A and Dec have the  same sign; sign [-] if pole and Dec have the opposite sign
(4) to find AO of a star A2 under the pole of A1, we calculate the  DA of A2 under the pole A1 ex: tan pôleA1.tan DecA2=sin DA A2/poleA1

The converse arc is 43.49°.

DP PLACIDUS	Plac direct	Plac conv
sa1/dm1	1,46	3,58
sa2	124,14	103,70
x	85,05	28,99
dm²	34,71	71,05
sign	-1	-1
-------------------------------------------------------------------
arc	-50,34	42,06
-------------------------------------------------------------------
FOMALHAUT-CHOISNARD
X = sa2.dm1/sa1
sign : if the two points are on either side of the meridian, take +1 ; otherwise -1

----------------------------------------------------------------------------------------------------------------------------
The Placidus converse arc is 42.06 Y (placidus arc = 40.41 Y).

DIRECTION ON AUGUST 2020

In August 2020, in the days leading up to the poisoning, Navalny had been publishing videos on his YouTube channel in which he expressed support for the pro-democracy 2020 Belarusian protests, which were triggered by the heavily contested 2020 Belarusian presidential election. Navalny had also written that the kind of 'revolution' that was taking place in neighbouring Belarus would soon happen in Russia.

Here we find several directions affecting the MC, in relation to // MA and JU since there is a conjunction between these two points (just as there is, I remind you, a conjunction between // SA and ME).

AR DIRECTIO || ♂ ☌ MC

AR MC = 87.49
AR || MA = 42.93
arc = 44.56 Y

DIRECTION ON 16 FEBRUARY 2024

1)- conversa directio ◻ ♀ ☌ ♂

It is one of the two directions coinciding with death. It hits the alchocoden.

speculum	Lat	Dec	AR	MD	SA	HA
MA	1,44 N	18,91 N	133,65	46,16 D	120,76 D	74,6 E
□VE	0 S	3,8 N	171,19	83,7 D	95,69 D	11,99 E

– MD = meridian distance (from MC if SA f [MA]  is diurnal or IC if Sa f  is nocturnal)
– SA = semi-arc (if f is diurnal, SA f [MA] is D and all MD’s and SA’s are D, otherwise N
– HA = horizontal distance (from the nearest horizon W or E for f [MA] and m □VE)
under bracket [] the fixed point, (here MA)
----------------------------------------------------------------------------------------------------------------------------

DP REGIOMONTANUS			DP REGIO-CAMPA C		DP REGIO-CAMPA D
	A2 □VE	A1 MA	A1 MA	A2 □VE	A2 □VE	A1 MA
Tan A	tan dec/cos dm		26,31		31,18
B (1)	+LG-A or -LG+A		29,87		25,00
Tan C	cot DM.cos B/cos A		42,90		-6,67
Sin pole (2)	Cos C.sin LG		37,49		55,60
Sin DA (3)	Tan pole A1.Tan Dec A2 Tan pole A2. Tan Dec A1	DAP	15,23	2,92	5,57	30,03
AO (4)	AR ± DA		118,41	168,27	165,62	103,62
arc	AO1 – AO2			-49,86		62,00
				CONVERS		DIRECT

(1) B must be < ε
(2) sign of pole has the same sens of LG for DA Here, DA = DA/pole A
(3) [+] sign if pole A and Dec have the  same sign; sign [-] if pole and Dec have the opposite sign
(4) to find AO of a star A2 under the pole of A1, we calculate the  DA of A2 under the pole A1 ex: tan pôleA1.tan DecA2=sin DA A2/poleA1
----------------------------------------------------------------------------------------------------------------------------
The arc is converse : 49.86 Y (key EQU 49.84 Y).
----------------------------------------------------------------------------------------------------------------------------

DP PLACIDUS	Plac direct	Plac conv
sa1/dm1	1,14	2,62
sa2	120,76	95,69
x	105,63	36,58
dm²	46,16	83,70
sign	-1	-1
-------------------------------------------------------------------
arc	-59,47	47,12
-------------------------------------------------------------------
FOMALHAUT-CHOISNARD
X = sa2.dm1/sa1
sign : if the two points are on either side of the meridian, take +1 ; otherwise -1
Arc = dm2 ±sign.x

----------------------------------------------------------------------------------------------------------------------------
Converse arc : 47.12 Y (key Placidus = 45.4 Y).

2)- recta directio ☉ ☌ ♄

The second direction touches the hyleg.

speculum	Lat	Dec	AR	MD	SA	HA
SA	0,44 N	20,6 N	122,20	34,71 D	124,14 D	89,43 E
CSU	0,00	22,47 N	72,56	14,93 D	128,13 D	113,2 W

– MD = meridian distance (from MC if SA f [SA]  is diurnal or IC if Sa f  is nocturnal)
– SA = semi-arc (if f is diurnal, SA f [SA] is D and all MD’s and SA’s are D, otherwise N
– HA = horizontal distance (from the nearest horizon W or E for f [SA] and m CSU)
under bracket [] the fixed point, (here SA)
----------------------------------------------------------------------------------------------------------------------------

DP REGIOMONTANUS			DP REGIO-CAMPA C		DP REGIO-CAMPA D
	A2 CSU	A1 SA	A1 SA	A2 CSU	A2 CSU	A1 SA
Tan A	tan dec/cos dm		24,57		23,17
B (1)	+LG-A or -LG+A		31,61		33,01
Tan C	cot DM.cos B/cos A		53,51		-73,71
Sin pole (2)	Cos C.sin LG		29,61		13,48
Sin DA (3)	Tan pole A1.Tan Dec A2 Tan pole A2. Tan Dec A1	DAP	12,33	13,59	5,69	5,17
AO (4)	AR ± DA		109,87	58,97	78,25	127,37
arc	AO1 – AO2			50,90		49,12
				CONVERS		DIRECT

(1) B must be < ε
(2) sign of pole has the same sens of LG for DA Here, DA = DA/pole A
(3) [+] sign if pole A and Dec have the  same sign; sign [-] if pole and Dec have the opposite sign
(4) to find AO of a star A2 under the pole of A1, we calculate the  DA of A2 under the pole A1 ex: tan pôleA1.tan DecA2=sin DA A2/poleA1
----------------------------------------------------------------------------------------------------------------------------
The direct arc is 49.12 Y
----------------------------------------------------------------------------------------------------------------------------

DP PLACIDUS	Plac direct	Plac conv
sa1/dm1	8,58	3,58
sa2	124,14	128,13
x	14,47	35,83
dm²	34,71	14,93
sign	1	1
-------------------------------------------------------------------
arc	49,18	50,76
-------------------------------------------------------------------
FOMALHAUT-CHOISNARD
X = sa2.dm1/sa1
sign : if the two points are on either side of the meridian, take +1 ; otherwise -1
Arc = dm2 ±sign.x

----------------------------------------------------------------------------------------------------------------------------
The arc is almost identical to that of Regio = 49.18 Y (Placidus key = 47.4 Y).

SOLI-LUNAR PHASE

---------------------------------------           
This is a method that we find outlined in Vettius Valens [book VI 9] as indicated by Anthony Louis in his blog :             
 'Vettius Valens had a different notion of annual returns. He felt that the return of the Sun each year was insufficient for forecasting for the year ahead because it omitted the influence of the the Sun’s partner, the Moon. As a result, Valens used a hybrid chart for the annual return which consisted of the positions of the planets when the Sun returned to its natal position each year but these positions were placed in a chart whose Ascendant and houses were determined by the moment the Moon returned to its natal degree during the zodiacal month when the Sun was in its birth sign.' [The Tithi Pravesh and its Monthly and Daily Iterations, November 5, 2022]             
Placidus uses it in his Primum mobile (Tabulae primi mobilis cum thesibus et canonibus 1657) and gives the procedure to follow in the XL canon (De Progressionibus, p. 53). A complete example appears in the analysis of the theme of Charles V (Exemplum Primum Caroli V. Austriaci Imperatoris, pp. 59-62).             
There is only one site on the internet that does this calculation:  https://horoscopes.astro-seek.com/calculate-planet-revolutions-returns/           
           
but it only gives the soli-lunar return at D0; Placidus continues the progression until end of process (i.e. even). For example in the case of NAVALNY Alexei, if we take the date of 16 Fev 2024, we must first translate this date into 'life-year equivalent': we find :           
---------------------------------------           
EVEN    47,7025943135195    47    Y
0    8,43113176223363    8    M
    12,933952867009    12    D
    22,4148688082159    22    H
        24,89    M
---------------------------------------           
The method of “embolismic lunations” as a predictive technique :              
An embolismic lunation, correctly termed an embolismic month, is an intercalary month, inserted in some calendars, such as the Jewish, when the 11-days' annual excess over twelve lunar months adds up to 30. An arbitrary application of this was used by Placidus, who applied the term Embolismic Lunation, to a Figure cast for the moment of the Moon's return to the same relation to the Sun that it occupied at birth. It was made the basis for judgment concerning the affairs and conditions of the ensuing year of life.' [https://astrologysoftware.com/community/learn/dictionary/lunation.html]              
The solar year does not have a whole number of lunar months (it is about 365/29.5 = 12.37 lunations), so a lunisolar calendar must have a variable number of months in a year. Regular years have 12 months, but embolismic years insert a 13th "intercalary" or "leap" month or "embolismic" month every second or third year [...]. Whether to insert an intercalary month in a given year may be determined using regular cycles such as the 19-year Metonic cycle [...] or using calculations of lunar phases [...]. [wikipedia]              
The whole difficulty therefore comes from the fact that there is no overlap between the solar month (30 D) and the lunar month (synodic month 29.53), consequently between the solar year (365.242) and the lunar year (354.367).            
 'In Vedic timekeeping, a tithi is a "duration of two faces of moon that is observed from earth", known as milа̄lyа̄ [...] in Nepal Bhasa, or the time it takes for the longitudinal angle between the Moon and the Sun to increase by 12°. In other words, a tithi is a time duration between the consecutive epochs that correspond to when the longitudinal angle between the Sun and the Moon is an integer multiple of 12°. Tithis begin at varying times of day and vary in duration approximately from 19 to 26 hours. Every day of a lunar month is called tithi.' [wikipedia]             
We see that the interest of Placidus' method (outlined by Vettius Valens) comes from the fact that the individualisation structure of the progression system is no longer represented by a single point (solar return or lunar return) but by a distance ( in this case the distance between SU radix and MO radix).           
We find in the literature another method which is similar to that of the solilunar phase: it is the tertiary directions. We find a critique of it in “Les Moyens de pronostic en Astrologie” by Max DUVAL [ed Traditionnelles, 1986, pp. 67-71] and a complete analysis in "A close look at tertiary progressions" by Elva Howson & Jack Nichols, [Considerations, vol XI-4, 1996; pp 3-12]- link           
In the case of NAVALNY Alexei, we observe:           
           
SU radix = 02° 06' 58" (2,12° ARI)           
           
MO radix = 80° 51' 45"° (80,86° GEM)           
           
∆ = |78° 44' 46"| (78,75° ) [ 6 tithi = ROUNDUP (∆/12)]           
           
Here is now the way in which Placidus would have proceeded: for 36 full years, 33 embolismic lunations are accomplished in 11 years after birth but with 33 days less, that is to say 11*3 since the moon covers 12 lunations in 11 days less than a whole year, as indicated in canon XL           
... if you wish to have a ready calculation of the progressions for several years, note that the moon does not complete twelve lunations in one whole year -i.e. a solar year - but in eleven days less. Having therefore the distance from the moon to the sun in the sky of birth, search for this eleventh day before the end of the first year of life and having found it, then know that the progression of twelve years of life is completed. Likewise 22 days before the end of the second year after birth gives the progressions accomplished for 24 years and so on' [De Progressionibus, op. cit., p. 54]           
Therefore on 4 JUN 1979, by removing 33 days, we arrive at 2 May 1979 [,,,] and then, the process is completed for 33 full years. Then, for the 11 other years elapsed during the twelve embolismic lunations, I arrive at 18 March 1980, for the remaining 10 months and 20 days. I compute the tithi (exact distance between SU and MO radix) for the last time : the date of Embolismic Progression J0 is : 22 March 1980at 12h 19min tu. Thereafter, i add to this date 20,75 d corresponding to 8,431M [see EVEN] :           
           
JD Pr Emb = 8,43 x 30 / (365.24 /29.53) = 20,75 D           
           
where 365.24 is the number of tropical days in a year and 29.53 is the average period for the synodic month of MO           
           
 trop days 365,242191120588 (1)           
           
syn month = 29,5305888021039 (2)           
           
where T = (JD-2451545)/36525           
           
In the present case JD = 2444320,5           
           
so, T = -0,235770020533881 (see formula 1 and 2)           
           
Finally, we find : date for J20,75D = 12 April 1980 at 11h 44min  local (6h 16min  TU).           
           
---------------------------------------           
(1) exact value for number of tropical days is : 365,2421896698-0,00000615359*T-0,000000000729*T^2+0,000000000264*T³           
(2) exact value for synodic month is : 29,5305888531+0,00000021621*T-0,000000000364*T^2   

       

We see We see a quasi conjunction between MOr and MAp (r = radix, p = phase). SUp is on point VIIIr. MOp is close to VI.
If we now give the mundane theme, we observe two counter-parallels between MA and the VE-SU group. We have a quasi-conjunction between SAr and MOp.

The way to interpret the double chart is not obvious: it is necessary to note above all the orientation of the houses and concerning serious events, observe XII and VIII. It also seemed to me that VE was often affected by counter parallels emanating from MA or SA. Once again, the interpretation is not unambiguous... It seems particularly interesting to study mundane charts in relation to their zodiacal side. In the case of NAVALNY, the problem is that his ordeal lasted a long time and it is not easy to establish a start date (his arrest, his conviction, his detention, the fatal change in prison?...)

If we take the date of 14 APRIL 2023 which corresponds to hospitalisation due to a significant worsening of his condition [link], we find :

SU radix = 22° 28' 29" (22,47° ARI)           
           
MO radix = 341° 21' 47"° (341,36° PIS)           
           
∆ = |318° 53' 17"| (318,89° ) [ 26 tithi = ROUNDUP (∆/12)]           
           
Here is now the way in which Placidus would have proceeded: for 36 full years, 33 embolismic lunations are accomplished in 11 years after birth but with 33 days less, that is to say 11*3 since the moon covers 12 lunations in 11 days less than a whole year, as indicated in canon XL           
... if you wish to have a ready calculation of the progressions for several years, note that the moon does not complete twelve lunations in one whole year -i.e. a solar year - but in eleven days less. Having therefore the distance from the moon to the sun in the sky of birth, search for this eleventh day before the end of the first year of life and having found it, then know that the progression of twelve years of life is completed. Likewise 22 days before the end of the second year after birth gives the progressions accomplished for 24 years and so on' [De Progressionibus, op. cit., p. 54]           
Therefore on 4 JUN 1979, by removing 33 days, we arrive at 2 May 1979 [,,,] and then, the process is completed for 33 full years. Then, for the 11 other years elapsed during the twelve embolismic lunations, I arrive at 18 March 1980, for the remaining 10 months and 20 days. I compute the tithi (exact distance between SU and MO radix) for the last time : the date of Embolismic Progression J0 is : 22 March 1980 at 9h 19min tu. Thereafter, i add to this date 20,75 d corresponding to 8,431M [see EVEN] :           
           
JD Pr Emb = 8,43 x 30 / (365.24 /29.53) = 20,75 D           
           
where 365.24 is the number of tropical days in a year and 29.53 is the average period for the synodic month of MO           
           
 trop days 365,242191120588 (1)           
           
syn month = 29,5305888021039 (2)           
           
where T = (JD-2451545)/36525           
           
In the present case JD = 2444341,5           
           
so, T = -0,235770020533881 (see formula 1 and 2)           
           
Finally, we find : date for J20,75D = 12 April 1980 at 8h 44min  local (3h 16min  TU).   

zodiacal chart

Here we find a true conjunction MOp-MAr ; a quasi-conjunction ASCr-SAp, MOp is conjunct to cusp of VIII.

The mundane chart (normalised to radix domification)  :

We find a true conjunction between MOp and SAr and another between VEp and MAr. We have also a counter-parallel between MAr and JUp. There is also a counter-parallel between JUr and VEp it is not a * because the mundane distance is 60). So we have a kind of mirror image in this chart.

 

CAMPANELLA Tommaso

05 Sep 1568 JUL CAL

sunday JUL

| lat 38° 29' 0" | N 16°28' E

0

---------------------------------

natal (bt) 15 h 27 min

raas-rams :0h 5' 0"

reckoned bt Lat --> lmt 6 h 16 min

tu 6h 16' 10"

tsn 5h 52' 38"

---------------------------------

timezone : 0

DST : 0 (-)

Equation of time 0h 5' 0"

ΔT 0h 2' 18"

---------------------------------

 Italian philosopher, theologian, astrologer, and poet.
Accused of leading a conspiracy against the Spanish rule in his hometown of Stilo, Campanella was captured and incarcerated in Naples (1599), where he was tortured seven times and then, crippled and ill, was sentenced to life imprisonment. Campanella spent twenty-seven years imprisoned there, often in the worst conditions. During his detention, he wrote his most important works including his most famous piece, The City of the Sun (originally written in Italian in 1602; published in Latin in Frankfurt (1623) and later in Paris (1638). He defended Galileo Galilei in his first trial with his work The Defense of Galileo (written in 1616, published in 1622). Campanella was finally released from prison in 1626, and was restored to full liberty in 1629. We note a whole series of trials against him between 1591 and 1594. That of 1599 earned him 26 years of captivity. Another plot almost succeeded in 1634.

He died on 21 May 1639 in the convent of Saint-Honoré in Paris, France.

source : "Una Nativita manoscritta di Campanella", Germana Ernst - Giuseppe Bezza, Bruniana & Campanelliana anno XIII, 2007/2, p. 711-716

 

 

Birth took place in Italy, in Stilo. The style is therefore italic: it is stipulated 12 6 HOR, that is to say about 6.16 (Sunset) + 12.6, at 6:26 pm, September 4. We must therefore count on September 5.

sunset 6,18 → [18,28]

italic : D-1 [pm: 6h 16' 42"]

For dates back to the 18th century, the day began at 0h of a real local solar time when the sun passed to the meridian of the place, which is close to the actual noon. We must therefore add 12 hours to find on this theme (and the many others which appear in this blog) our current civil time.

THEME

SU is P with a [-11] score
MO is Fa with a [-1] score
VE is F cb  with a [-4] score
JU is Ru with a [-5] score

MA is D with a [-8] score

SA is te - T with a [18] score
Moreover, SA is in mutual reception by exaltation with ME which is an unfortunate circumstance (cf, Morin de Villefranche, Astrologia gallica, book XVII, cap VII, 39-51, La Haye, 1636)
Last, ME is besieged (<13° between MA and SA) that is another unfortunate circumstance.

we see below the list of  aspects :
---------------------------------------
              JU 90 SU Or             MA 120 MO Oc                                JU 90 VE Or                
---------------------------------------
The best aspect is  [best :ma 0° (0,63) me]  and the worst aspect is  [worst :mo 120° (-0,03) ma]


The traditional almuten (Omar, Ibn Ezra) is JU
we see below the list of dignities for JU :
---------------------------------------
[ term 4 tri 0 rul 2 exn 0 fac 4 ]
[ su 2 mo 0 asc 3 syg 0 pof 2 ]
---------------------------------------
Note 1 : the ‘almuten figuris’ is the lord of the chart, but its determination obeys somewhat different rules according to the schools. The tradition is based above all on the zodiacal dignities. (see p,e,  Alcabitius, Introduction, 59-61, 117 and Avenezra, Nativites, 101) – almuten = al-mu’tazz (arabic term)
[7] As for the governor which is the <planet> predominating (al-mubtazz) over the birth from which one indicates the conditions of the native after the haylāğ and the kadhudāh,n it is the planet having the most leadership in the ascendant, the position<s> of the two luminaries, the position of the Lot of Fortune and the position of the degree of the conjunction or opposition which precedes the birth. When a planet has mastery over two, three or four positions by the abundance of its shares in them, it is the governor and the predominant <planet> (al-mubtazz) and the indicator after the haylāğ and the kadhudāh. From it one indicates the conditions of the native. Some people use it instead of the kadhudāh in giving life.  [Al-Qabisi , Charles Burnett, Keji Yamamoto, Michio Yano, The Introduction to Astrology, IV, 7, p, 117, Warburg, 2004]
Note 2 : There are at least 4 systems for determining the almuten depending on whether the combinations of triplicities and terms are used: the Ptolemaic almuten (followed by Lilly) with Ptolemaic terms ; the same with Egyptian terms; the almuten of Dorotheus with Ptolemaic terms ; the same with Egyptian terms, knowing that one can embellish the whole thing with different weighting system (like Lilly or not using weights like Montanus) [cf. Temperament: Astrology's Forgotten Key, p. 79, Dorian Gieseler Greenbaum 2005]

The Lilly (Ptolemaïc) almuten is SA

In our experience, it seems that Ptolemy's almuten allows one to first appreciate the static side of the natal chart and that the Lilly-type elaboration allows one to deepen the more ‘temporary’ or ‘dynamic ‘ relationships (cf, Shlomo Sela, Ibn Ezra, on Nativities and Continuous Horoscopy, appendix 6, quot 2  ; Horary astrology p, 458, Brill, 2014)
---------------------------------------
Ω  165,41 /
---------------------------------------

We note that Algol (bêta Persei) is conjuct (in mundo) with cusp of IX house... and TRINE to SA, conjuct to ASC. Unfortunately, this did not prevent accidents and severe injuries. Antares is conjuct (in mundo) with JU : "Great religious zeal, real or pretended, ecclesiastical preferment, a tendency to hypocrisy, benefits through relatives" [Fixed Stars and Constellations in Astrology, Vivian E. Robson, 1923, p.136, 234].

HYLEG - ALCHOCODEN

ZODIACAL – MUNDANE

In our research, we hypothesized that the mundane chart alone should be considered; also we must base on the aspects taken in the semiarcs the research of the degrees likely to be considered in the duration of the life.
In the case of CAMPANELLA Tommaso we have the table above which allows us to estimate the breakdown of aspects between the different planets and the alchocoden.
When considering a theme, the first thing is to observe whether it is diurnal or nocturnal. In the case of CAMPANELLA Tommaso, it is .
In this case, the first point to check is SU. If  SU is well disposed, it can claim 1st stage to be HYLEG.

SU is P and therefore seems weak, with a dignity score of [-7],
But, when we look for the dignities that appear in the zodiacal inscription of ASC, we find none.
we find at least one aspect to match with the dignities
We'll see later what we get when we search for mundane dignities.
Now that we doubt to take SU as hyleg, we are left with MO but we don't find any aspect to match with the dignities,,,

Now that we doubt to take MO as hyleg, we are left with the choice of ASC and that of POF. It is the way in which is laid out MO which will indicate the choice to us. If MO is waxing, we take ASC for hyleg ; if MO is waning, we take POF for hyleg,

It turns out that MO is waxing; so we will take ASC,
Now we must look for the alchocoden: it is the planet which has the maximum dignity with regard to the hyleg and which exchanges a Ptolemaic aspect with the hyleg.
if we consider the MUNDANE system, we observe a conjunction aspect of SA.
At the same time, it appears that SA has  dignity of TERM over ASC.
So we have two possibilities with our hypothesis : first choose ASC for hyleg ; second choose the MUNDANE system and try to find another couple of hyleg/alchocoden,
 If we choose now ASC we must know that Dorotheus, Al Qabisi, and Ptolemy, agree with this choice
In case of ASC is the Hyleg, there is then one candidate to be the alchocoden:SA
First, we have to see which candidate has the most dignity: here, SA has candidate alcho dignities referring to ASC : [TERM]
First, SA is linked with ASC by a [conjunction] aspect and a [TERM] dignity,
However, SA is [te - T] and has a power of [3], SA has a Kadkhudah score of [1]
SA is located at 179,21 °at more than 5° from [Δ degrees cups sup [XII] : 29,41° (330)] and has a domitude regio of : [359,41] for a latitude of [2,13°]

So, HYLEG = ASC and ALCHOCODEN = SA.

DIRECTIONS AT DEATH

DIRECTIO DIRECTA (m) □ ♄ ☌ ☽

---------------------------------------------------------------------------------------------------------------------

DP REGIOMONTANUS			DP REGIO-CAMPA D		DP REGIO-CAMPA C
	A2 □SA	A1 MO	A1 MO	A2 □SA	A2 □SA	A1 MO
Tan A	tan dec/cos dm		-18,29		-23,48
B (1)	+LG-A or -LG+A		20,19		15,00
Tan C	cot DM.cos B/cos A		-18,35		89,80
Sin pole	Cos C.sin LG		36,20		0,13
Sin DA (2)	Tan pole A1.Tan Dec A2 Tan pole A2. Tan Dec A1	DAP	-4,41	-18,54	-0,06	-0,01
AO (3)	AO ± DA		335,20	249,84	268,32	339,60
arc	AO1 – AO2			85,36		71,28
				DIRECT		CONVERS

 --------------------------------------------------------------------------------------------------------------------

DP PLACIDUS
METHOD CHOISNARD
	Plac direct	Plac conv
sa1/dm1	524,81	1,33
sa2	94,80	110,21
x	0,18	83,06
dm²	71,45	0,21
sign	-1	-1
-------------------------------------------------------------------
arc	71,27	-82,85
-------------------------------------------------------------------
X = sa2.dm1/sa1
sign : if the two points are on either side of the meridian, take +1 ; otherwise -1
Arc = dm2 ±sign.x

----------------------------------------------------------------------------------------------------------------------

We note a whole series of trials against him between 1591 and 1594. That of 1599 earned him 26 years of captivity.

'At Naples. however, suspicions and allegations regarding the young friar were also taking shape. In 1592, the ‘first trial’ took place, an event that was still obscure and uncertain in the treatment of Amabile and then later took on more precise contours in the studies of Giovanni Gentile and Luigi Firpo. In the month of May, Campanella was imprisoned in the convent of San Domenico, on the allegation that his extraordinary knowledge had a demonic origin and that he had scoffed at excommunication. But the real issue, as would later be verified from the text of the condemnation, was adherence to the doctrines of Telesio.' [Germania Ernst, Tommaso Campanella: The Book and the Body of Nature, p. 19, Springer, 2010]

DIRECTIO CONVERSA : [c] (m) □ ♄ ☌ ♂

This direction may seem paradoxical because it involves the two malecient planets. However, let us not forget that SA is alchocoden, in close conjunction with ASC. What we observe is a singular ballet of arcs engaging the square of Saturn: one with a direct direction to MO, the other with a converse direction to MA (which will have had the last word in this epic battle of a life!).

speculum	Lat	Dec	AR	MD	SA	HA
MA	-0,07 S	-10,59 S	205,28	62,88 N	98,55 N	35,67 E
□SA	0 S	-23,48 S	268,37	0,21 N	110,21 N	110 W

– MD = meridian distance (from MC if SA f [MA]  is diurnal or IC if Sa f  is nocturnal)
– SA = semi-arc (if f is diurnal, SA f [MA] is D and all MD’s and SA’s are D, otherwise N
– HA = horizontal distance (from the nearest horizon W or E for f [MA] and m □SA)
under bracket [] the fixed point, (here MA)
 --------------------------------------------------------------------------------------------------------------------

DP REGIOMONTANUS			DP REGIO-CAMPA C		DP REGIO-CAMPA D
	A2 □SA	A1 MA	A1 MA	A2 □SA	A2 □SA	A1 MA
Tan A	tan dec/cos dm		-22,30		-23,48
B (1)	+LG-A or -LG+A		16,18		15,00
Tan C	cot DM.cos B/cos A		-28,00		89,80
Sin pole (2)	Cos C.sin LG		-33,33		-0,13
Sin DA (3)	Tan pole A1.Tan Dec A2 Tan pole A2. Tan Dec A1	DAP	7,06	16,60	0,06	0,02
AO (4)	AO ± DA		212,34	284,97	268,32	205,26
arc	AO1 – AO2			-72,63		63,06
				CONVERS		DIRECT

(1) B must be < ε
(2) sign of pole has the same sens of LG for DA Here, DA = DA/pole A
(3) [+] sign if pole A and Dec have the  same sign; sign [-] if pole and Dec have the opposite sign
(4) to find AO of a star A2 under the pole of A1, we calculate the  DA of A2 under the pole A1 ex: tan pôleA1.tan DecA2=sin DA A2/poleA1
 --------------------------------------------------------------------------------------------------------------------

directio conversa	(AR C MA – AR fc) – HD□ SA x Temp HC MA	(AR □ SA – AR fc) – HDC MA x Temp H□ SA
-1
Al-Battani, adapted from Nallino, Opus astronomicum, pp, 315-317	□ SA [S W]	C MA [S E]
ar signif	268,37	205,28
meridian : □ SA [IC | C MA [IC]	88,16	88,16
1	0,21	117,12
Dec	-23,48	-10,59
dAR	-20,21	-8,55
hd prom	3,83	0,01
temp H signif	18,37	16,42
arc	70,54	-63,07

 --------------------------------------------------------------------------------------------------------------------
The arc is 70.54 Y (the Placidus key gives 72.7 Y).

Hd prom=6.MD prom/SA prom	Hd sign=6.MD sign/SA sign
3,83	0,01
Temp H prom = (90-dAR prom)	Temp H sign = (90-dAR sign)
18,37	16,42
pm placidus
0,18	57,43
dom	dom
90,18	32,57

 --------------------------------------------------------------------------------------------------------------------

DIRECTION FOR MAY 1592

We see a # SU conj MA. It is the first of a whole series of trials against him between 1591 and 1594. That of 1599 earned him 26 years of captivity.It is the first in a series of counter-parallels related to the stellium of SU with [ME VE SA] which frames the ASC. Moreover, we see that MA is besieged (see Bonattus, Decem continens tractatus astronomie in Liber Astronomiae, part III, trad Robert Hand, cap XXI, pp. 96-97, Project Hindsight, vol XI, 1995).

DIRECTIO CONVERSA ♯ ☉ ☌ ♂

We must take into account an important element: the ascensional difference (DA). This is the difference between Right Ascension (AR) and Oblique Ascension (OA). DA is always calculated in absolute value |DA| and it is added or subtracted from 90° (SA = 90° corresponds to a point on the equator cut by the horizon; depending on whether a star approaches or moves away from the line of horizon, SA is > 90° or < 90°, i,e, (+) depending on whether it is diurnal and northern ; or nocturnal and southern ; (-) depending on whether it is diurnal and southern ; or nocturnal and northern. But we have to take care of a fact : when we have a counter parallel or an aspect, the quadrant is not the same and the declination is different ; so the sign is also different.

sin(DA) = -tan(φ)tan(δ)
φ = latitude 38,48 N
δ MA = -10,59 -
DA-MA = 8,55°
δ (m) #SU =-2,37 -
DA-(m) #SU =1,89°

-------------------------------------------------------------------------------------------------------------------------

converse direction	Lat	Dec	AR	MD	SA	HA
MA	-0,07 S	-10,59 S	205,28	63,63 N	98,55 N	34,92 E
(m) #SU	0,00	-2,37 S	185,46	83,45 N	91,89 N	8,44 E

-------------------------------------------------------------------------------------------------------------------------

– MD = meridian distance (from MC if SA f [MA]  is diurnal or IC if Sa f  is nocturnal)
– SA = semi-arc (if f is diurnal, SA f [MA] is D and all MD’s and SA’s are D, otherwise N
– HA = horizontal distance (from the nearest horizon W or E for f [MA] and m (m) #SU)
under bracket [] the fixed point, (here MA)

DP REGIOMONTANUS			DP REGIO-CAMPA C		DP REGIO-CAMPA D
	A2 (m) #SU	A1 MA	A1 MA	A2 (m) #SU	A2 (m) #SU	A1 MA
Tan A	tan dec/cos dm		-22,83		-19,94
B (1)	+LG-A or -LG+A		61,31		58,42
Tan C	cot DM.cos B/cos A		-14,48		3,66
Sin pole	Cos C.sin LG		37,05		38,39
Sin DA (2)	Tan pole A1.Tan Dec A2 Tan pole A2. Tan Dec A1	DAP	-8,11	-1,79	-1,88	-8,52
AO (3)	AO ± DA		213,40	187,25	187,34	213,80
arc	AO1 – AO2			26,14		26,46
				CONVERS		DIRECT

To obtain the arc of direction between two signifying points (planets in body, aspect versus planet, planet versus axis) one must find AO (oblique ascent) of f and of m, calculated under the pole of f.
The formulas to use can be found either in the ‘Dictionnaire astrologique’ of Henri Joseph Gouchon (Dervy Livres, 1937) pp. 266-267, or in his ‘Horoscope annuel simplifié’ (Dervy, 1973) p.181. Other formulas can be found in ‘Les moyens de pronostic en astrologie’, Max Duval (editions traditionnelles, 1986) and ‘Domification et transits’ (Editions traditionnelles, 1985). We can also cite by André Boudineau : ‘Les bases scientifiques de l’astrologie’ (Chacornac, 1937) These are references in French but there are many other references in English or German of a less obvious but equally valid use.

First, compute the ascensional difference under f (MA) : cot DAP f = (cot de f x cot lat) / in DM f ± cot DM f, i,e, :  cot (DAP f) = (Cot dec f[-10,59°] x Cot Lat [38,48°]) /sin DM f [63,63°] ± cot DM f  [63,63°]

DAPf = 171,89°

We find the pole of f (MA) by formula : tan(pole f) = sin (DAP f) x cot (dec f) i,e, tan(pole f) = tan f [8,11°] x cot f [-10,59°]

pole MA regio  =-37,05°

(1) We need now the DAP of m ((m) #SU) under the pole of f, sin (DAP m) = tan (pole f) x tan (DEC m), i,e, : (MA) : sin (DAPm/f) = tan [37,05°] x tan [-2,37°]

DAP m/f = -1,79°

then we find for the points located in the eastern part of the chart : AO f = AR f± DAP f ; sign (+) if Dec f boreal or sign (–) if Dec f Austral ; so : AO f MA = 213,4° and AO m = AR m ± DAP m ; idem for sign ; so  AO m(m) #SU = 187,25°

---------------------------------
arc D Regio = 26,14°
---------------------------------
We are now going to compute the converse Regiomontanus direction corresponding to the arc  f MA / p (m) #SU

First, compute the ascensional difference under m ((m) #SU) : cot DAPm = (cot dec m x cot lat)/sin DM m ± cot DM m, i,e, :  Cot(DAP m) = (Cot decm[-2,37°] x Cot Lat [38,48°]) / Sin DM f [83,45°] ± Cot DM m [83,45°]

DAP m = 178,12°

We find the pole of m ((m) #SU) by formula : Tan(pole m) = Sin (DAP m) x Cot (dec m) i,e, Tan(pole m) = Sin m [178,12°] x Cot m [-2,37°]

pole (m) #SU regio  =-38,39°

We need now the DAP of f (MA) under the pole of m, Sin (DAP f) = Tan (pole m) x Tan (DEC f), i,e, : ((m) #SU) : Sin (DAP f/m) = Tan[38,39°] x Tan [-10,59°]

DAP f/m = -8,52°

then we find for the points located in the eastern part of the chart : AO m = AR m ± DAP m ; sign (+) if Dec m boreal or sign (–) if Dec m Austral ; so : AO m (m) #SU = 187° and AO f = AR f ± DAP f ; idem for sign ; so  AO f MA = 213,8°

---------------------------------
arc C Regio = 26,46°
---------------------------------
H.J. Gouchon [l’Horoscope Annuel simplifié, Dervy, 1973, p, 181-182 and Dictionnaire astrologique, p, 277, 1937-1942, Gouchon ed., 1975, Dervy, but be careful because in DAP's equation, the double sign ± was mistakenly replaced by the sign (-) ] advises to avoid errors, to always place the star A1 (for us f, i.e. SU) in the eastern houses; in fact it is enough to change the registration number of the house based on the transformation (IV-V-VI) -> (X-XI-XII) and (VII-VIII-IX) -> (I-II-III ) to adapt the double sign ± in the calculation of DAP f or DAP m; moreover, this sign must be reversed if |DM| > 90°.

For the Regiomontanus directions, there is another mode of computing, mentioned by Gouchon (Dictionnaire astrologique, op. cit., p. 276) and especially Martin Gansten (Primary directions, pp. 155-157, the Wessex Astrologer, 2009)
This method consists at computing first 3 auxiliary angles before  the pole. It then joins the other method. Contrary to what Gouchon says, I find it easier than the previous one because we avoid the double sign ± in the determination of DAP f.

So, initially, we have A => Tan f = tan dec f [-10,59°] / cos DM f [63,63°]

A = -22,83°

Then : B = Lat [38,48°] + A [-22,83°]

B = 61,31°

And, Tang C = Cot DM f [63,63°] x Cos B [61,31°] / Cos A [-22,83°]

C = -14,48°

Then, we have Sin pole f = Cos C [-14,48°] x  Sin LG [38,48°]
---------------------------------
So, pole MA regio = 37,05°
---------------------------------
Now go back to (1)

For m (m) #SU; we have : A => Tan m = tan dec m [-2,37°] / cos DM m [83,45°]

A = -19,94°

Then : B = Lat [38,48°] + A [-19,94°]

B = 58,42°

And, Tang C = Cot DM m [-263,45°] x Cos B [58,42°] / Cos A [-19,94°]

C = 3,66°

Then, we have Sin pole m = Cos C [3,66°] x  Sin LG [38,48°]
---------------------------------
So, pole (m) #SU regio = 38,39°
---------------------------------

DP PLACIDUS	Plac direct	Plac conv
sa1/dm1	1,10	1,55
sa2	98,55	91,89
x	89,50	59,33
dm²	63,63	83,45
sign	-1	-1
-------------------------------------------------------------------
arc	-25,87	24,12
-------------------------------------------------------------------
FOMALHAUT-CHOISNARD
X = sa2.dm1/sa1
sign : if the two points are on either side of the meridian, take +1 ; otherwise -1
Arc = dm2 ±sign.x

We will now use the Placidus system of mundane directions. The simplest system is that of Choisnard-Fomalhaut. First you need to retrieve the data from the SA (semi-arc) and the DM (meridian distance) of the nocturnal point because the altitude of MA is -27,14°. important note: the SA and DM of the two points are always counted diurnal if the first point (here MA) is above the horizon even if the second is below. They are counted nightly if the first point (MA) is below the horizon regardless of the position of the second point.
For DMs, they are counted in AR from the diurnal meridian if the fixed point MA is diurnal, and from the nocturnal meridian if it is nocturnal.

nocturnal meridian MC = 268,91°
AR MA = 205,28°
AR (m) #SU = 185,46°

SA N (δ-) (m) #SU = 91,89°
DM N  (m) #SU = 83,45°

For the  significator  (m) #SU altitude (h) =-6,6°. so :

SA D (δ-) (m) #SU = 98,55°
DM N  MA = 83,45°

Then we compute Saf/DMf (so : SA f [ 91,89°] / DM f [ 83,45°])

Sa f / DM f =1,1

and the angle x = SAm x DM f/SA f, so : SA m [ 98,55°] x DM f [ 83,45°]/SA f [ 91,89°]

 x = 89,5°

We find the direction by DMm - x, so : DM m [ 83,45°] ± x [89,5]
We must now have regard to the double ± sign of the last expression; in the case where f (MA) and m ((m) #SU) are on either side of the meridian, the direction arc is obtained by taking the sum (instead of the difference) of the two quantities DMm and x. This is not the case here, so sign = (+)
the computation of the arc requires, depending on the case, a reduction of 360° (so arc modulo 360°)
---------------------------------
arc D =-25,87°
---------------------------------
in the technical sense, It is a direct direction but in the astrological sense, it is a true converse direction since it is an aspect considered as a promissor which goes towards the significator. ; so the m point is an aspect (here (m) #SU) and the f point is a planet or an axis, (here MA)

We can now compute the converse direction : point f is directed towards point m, i.e. the star is directed towards the aspect. This is where the problem of the orientation of the primum mobile arises because it is not concevable to rotate the local sphere in both directions… It does not seem convenient to postulate that the arc of direction is counted in the order of the signs of the zodiac (when it is direct, i.e. when one directs a promissor towards a significator): indeed, the ecliptic has nothing to do with a direction since this one depends only on the diurnal movement ( primum mobile). It is therefore otherwise that we must pass judgment on this.

That time, we compute Sa m / DM m (so : SA m [81,45] / DM m [116,37])

Sa m / DM m =1,55

and the angle x = SA f x DM m/SA m, so : SA f [ 91,89°] x DM m [116,37] / SA m [81,45]

x = 59,33°

We find the direction by DM f - x, so : DM f [ 83,45°] ± x [59,33°]
We must now have regard to the double ± sign of the last expression; in the case where m ((m) #SU) and f (MA) are on either side of the meridian, the direction arc is obtained by taking the sum (instead of the difference) of the two quantities DM f and x. This is not the case here, so sign = (-)
---------------------------------
arc C =24,12°
---------------------------------
Below we will find two algorithms that we find in the Encyclopedia of Islam (vol IV, 1934) in the article tasyir and in the translation given by Carlo Alfonso Nallino of the opus astronomicum of Al-Battani (1903)

	Adapted from Schirmer, 1934 [al-Battani, al-Biruni]		directio conversa
	AR (m) # SU - ARC MA		1
	19,82	19,82
	OA (m) # SU - OAC MA
	26,48	26,48
	dist C MA from FC	-63,63
	-63,63	83,45
	half night arc C MA (= SA)	-360
	98,55	91,89
	tasyir degrees
	24,12	25,87
	335,879	385,87

"According to the respective positions of the significator and promissor, two kinds of tasyir arc distinguished:

a. Direct tasyir (directio directa) when the significator precedes the promissor in the order of the signs of the zodiac. Here the significator is the place to be “directed”, the promissor regarded as fixed .

b. Indirect tasyir (directio conversa) when the significator precedes the promissor in the order of the daily motion of the celestial sphere. In this case the promissor is moved to the circle of position of the significator which is assumed to be fixed.

A special form for application of the calculation of the tasyir (a kind of inversion of the process) was developed in choosing days in this way that the position of only one star was given and also a definite time or what is the same thing on account of the conversion of periods of time into degrees of the equator, a definite number of tasyir degrees. The problem is to find the degree which corresponds to the end point (the “goal”) of the tasvir arc. indicia could then be deduced from the conjunction of planets occurring at this degree." [Schirmer, in Encyclopaedia of Islam, vol IV, article :AL-TASYIR (in the west; atazir, atagir, athadr, directio, prorogatio, théorie aphétique, pp. 694-697, 1934),

Al-Battani, adapted from Nallino, opus astronomicum, pp, 315-317	(AR C MA – AR fc) – HD(m) # SU x Temp HC MA	(AR (m) # SU – AR fc) – HDC MA x Temp H(m) # SU
ar signif	185,46	205,28
	SU	MA
ar cardine	88,91	88,91
1	96,55	116,37
Dec	-2,37	-10,59
dAR	-1,89	-8,55
hd prom	3,87	5,45
temp H signif	15,31	16,42
arc	155,86	205,84
	24,14	-25,84

But there is another kind of direction which is entirely consistent with tradition; it consists of directing (in the direction of the signs of the zodiac) the planet to the aspect (or parallel). We practice this category of directions in mundo.

ANOTHER DIRECTIO # ♂ ☌ ☉

 

This direction is superimposed on the previous one: I call it an “echo” direction. This type of leadership often demonstrates lasting episodes.

DIRECTION FOR 1592

We find the two same with a smaller orb.

Much more serious was the Calabrian plot in 1599 : arrestation the 6 September 1599.

DIRECTION FOR SEPTEMBER 1599

We find a square MO to MC (diff AR 1.22°).

We note two counter parallels echo: # SA conj MA and # MA conj SA.

DIRECTIO #MA conj SA

This direction touches SA, the alchocoden. It is all the more important as SA is close to ASC (AO ASC = 179.16°) and AO SA = 178.32°. We note that AO # MA is 177.54°.

We find the arc with the method of MAGINI :

MAGINI – REGIOMONTANUS   
direct   
--------------------------------------------------------------------------------------------------------------------------

speculum	Lat	Dec	AR	MD	SA	HA
SA	2,13 N	2,27 N	180,13	90,97 D	91,81 D	0,84 E
(m) #MA	-0,07 S	10,97 N	153,32	64,16 D	98,86 D	34,7 E

--------------------------------------------------------------------------------------------------------------------------    – MD = meridian distance (from MC if SA f [SA]  is diurnal or IC if Sa f  is nocturnal)
– SA = semi-arc (if f is diurnal, SA f [SA] is D and all MD’s and SA’s are D, otherwise N
– HA = horizontal distance (from the nearest horizon W or E for f [SA] and m (m) #MA)
under bracket [] the fixed point, (here SA)
 
modified from [ Delambre, Hist Astron Moyen Âge, Magini, pp, 486-491 Paris 1819]   
    
    Eq for Fig 129 (pl 12)  see fig for location and explanation of spherical triangles
   

    h (altitude  of the promissor) - H (latitude of the observer) - D (declination of the promissor) –
    D' (declination of incident horizon = position circle of promissor) - PH=H -

Problem XVI gives the means of finding if a star is in the same circle of position, with a planet or any significator. Find the arc position ET, which assumes the hour angle of the star and its semidiurnal arc. With ET and H you will have the angle O of the position circle with the meridian; you will compare this circle to that of the significator and you will see if it differs from it. Problem XVII. The significance being placed in
any angle, direct or lead him to the promissor, following the order of the signs. He [Magini] calls, following the usage of astrologers, significator, the one who holds the first place in the zodiac, and promissor, the one who holds the second place according to the order of the signs.
 To direct means to seek the arc of the equator which, by the movement of the sphere, while the promissor will be transferred to the position of the first, that is to say of the significator, will pass through the meridian or through the horizon, if it is in one of these circles, or through the circle of position of the significator, if it declines from one of these angles. We have already seen that astrologers counted four angles; the angle of the east and that of the west, that of the upper meridian and that of the lower meridian; that is to say the two points of the ecliptic which are on the horizon and the two which are at the meridian. The angle of the upper meridian was also called the middle of the sky, that of the lower meridian was still called the bottom of the sky. This problem, quite complicated, depends only on the most ordinary rules of spherical trigonometry. [DELAMBRE, Hist Astron Moyen-Âge
Extracted and adapted from pp, 486-491]

control pole (0,1) necessary to calibrate the type of direction.
P (horary angle, from midnight)    0
-64,16    ||  cosP = (sinh-sin Hsin D)/(cosHcosD)
295,84   
PHA (HAO angle)   
-62,84    ||  TanPHA = sinP/((sinD+cosP)cosH)
------------------------------------------   
PR (pole HAO)   
-33,619    ||  sinPR=sinPHsinPHA
    
ET (arc meridian/HAO)   
123,24    ||  tanET=cosHtanPHA
------------------------------------------    MAGINI – PROBLEMA XVI
H'    ||  H' (incident horizon = B50
33,62    ||  tanH'=sinETtanH
------------------------------------------   
PAR (position angle)   
34,33    ||  sinPAR=sinH'/cosD
    
QS, HPR (Az PR)   
33,24    ||  cosQS=sinET
    
ΔAR' (DA/HAO)   
7,40    ||  sinΔAR'=tanDtangH'
    
OTE, HTQ, ETH (equat/HAO angle)   
56,38    ||  tanOTE=cotH/sinET

Problem XVIII. Wherever the signifier is, outside the angles from the meridian and the horizon, lead him to any promissor, following the order of the signs, by the rational path. The operation, says Magini, is very painful. You must have right ascension and the distance to the meridian, both of the significator and the promissor; their declinations and the semi-diurnal or semi-nocturnal arc, depending on whether it is above or below the horizon; it is necessary to find the elevation of the pole on the position circle and the position arc. We reported the necessary formulas for all these calculations. Then let S be the signifier, R the promissor (fig. 130), RZN the parallel of the promissor, OK the difference of
 right ascensions; R will cross the ASC position circle in Z; K.V will be the movement of the equator, which will take R to point Z; the time interval will be therefore measured by

KV = KO — OT — TV = direction,

These last problems bring the theory of directions into the greatest light ! This theory belongs exclusively to the Middle Ages. No one has exposed it as completely as Magini. [DELAMBRE, Hist Astron Moyen-Âge Extracted and adapted from pp, 486-491]

------------------------------------------    MAGINI – PROBLEMA XVII
KO (≠AR (m) # MA C SA)    Eq for Fig 130 (pl 12) see fig for location and  Explanation of spherical triangles
26,81    ||  KO=AR(m) # MA - ARC SA
------------------------------------------   
A (AET angle)    ||  EA = 90-H
62,84    ||  sinA=sinETsinOTE/sinEA
    MAGINI – PROBLEMA XVIII
T (angle horizon/OTH)    ||  pole of PRS (=90-H')
56,38    ||  cosT=sinAETsinH
    
[+] TO ΔAR' (m) # MA    ||  D boreal --> sign OT [+]
7,40    ||  sinTO=tanDcotT
1    +
[-] TV ΔAR' C SA    ||  D' boreal-> sign TV [-]
1,51    ||  sinTV=tanVZcotT
-1    -
tasyir    ||  If OS (D) [+], TO ~ sign,  If RK (D') [-], TV ~ sign
32,70    ||  KV=KO – OT – TV
    
VZ    ||  D' (declin of C SA)
2,27   
    
OS    ||  D (declin of (m) # MA)
10,97   
    
ST    distance ST
13,21    ||  sinST=sinD/sinT
    
TZ    distance TZ
2,73    ||  sinTZ=sinD'/sinT
    
ZS    ≠dist
10,48    ||  If D/D'<0 [-]
    
EPA (EPV, EV) ± ΔAR'    horary angle of (m) # MA
130,65    ||  if d is [-] ~ ΔAR'
    
IOANNIS ANTONII MAGINI  PRIMI MOBILIS LIBER NONUS QUI AGIT DE DIRECTIONIBUS pp, 214-232 PROBLEMA XVI p, 229 – PROBLEMA XVII p,229  PROBLEMA XVIII p, 230 Venezia: Damiano Zenaro. 1604   

So, we see that arc = 32.7 Y.

PLACIDUS

	(AR C SA – AR mc) – HD(m) # MA x Temp HC SA	(AR (m) # MA – AR mc) – HDC SA x Temp H(m) # MA
Al-Battani, adapted from Nallino, Opus astronomicum, pp, 315-317	(m) # MA [N E]	C SA [N E]
ar signif	153,32	180,13
meridian : (m) # MA MC] | C SA [MC]	89,16	89,16
1	64,16	90,97
Dec	10,97	2,27
dAR	-8,86	-1,81
hd prom	5,95	3,89
temp H signif	16,48	15,30
arc	-33,81	31,39

Hd prom=6.MD prom/SA prom	Hd sign=6.MD sign/SA sign
-5,95	3,89
Temp H prom = (90-dAR prom)	Temp H sign = (90-dAR sign)
16,48	15,30
pm=90*DM/SA
58,41	-89,18
domitude placidus=(3±dm/sa)*90	(3±dm/sa)*90
328,41	359,18

the formula for domitude varies if h>0 or h<0 (± modulo 360 and take dm and sa for the correct quadrant). Max Duval (la domification et les transits, Ed Traditionnelles, 1984) gives an incomplete formula for domitude, only the formula of pm).
If h<0, dom placidus = (1+dm/sa)*90
If h>0, dom placidus = (3+dm/sa)*90

For #MA, dom pla = 90*(3+dm/sa) and for SA, dom pla= 90*(3-dm/sa) ; here take dm from mc for both and diurnal semi-arc for both.

Take the arc = 31.39 Y for directio directa. The placidus key gives : 32.3 Y.

LIBERATION : MAY 1626

DIRECTIO (m) ∆ ♀ ☌ ☽

----------------------------------------------------------------------------------------------------------------------

speculum	Lat	Dec	AR	MD	SA	HA
MO	2,41 N	-5,99 S	339,65	72,26 N	94,21 N	21,95 W
*VE	1,42 N	-21,18 S	286,60	17,44 N	107,94 N	90,5 W

----------------------------------------------------------------------------------------------------------------------

DP REGIOMONTANUS			DP REGIO-CAMPA C		DP REGIO-CAMPA D
	A2 *VE	A1 MO	A1 MO	A2 *VE	A2 *VE	A1 MO
Tan A	tan dec/cos dm		-16,87		-22,10
B (1)	+LG-A or -LG+A		21,61		16,38
Tan C	cot DM.cos B/cos A		-17,27		73,12
Sin pole	Cos C.sin LG		36,45		10,41
Sin DA (2)	Tan pole A1.Tan Dec A2 Tan pole A2. Tan Dec A1	DAP	-3,91	-16,63	-4,08	-0,97
AO (3)	AO ± DA		337,50	269,97	282,52	340,45
arc	AO1 – AO2			67,53		57,92
				CONVERS		DIRECT

(1) B must be < ε
(2)to find AO of a star A2 under the pole of A1, we calculate the  DA of A2 under the pole A1 ex: tan pôleA1.tan DecA2=sin DA A2/poleA1
(3) [+] sign if pole A1 and Dec A1 have the  same sign; sign [-] if pole A2 and Dec A2 have the opposite sign
----------------------------------------------------------------------------------------------------------------------

The direct arc is 57.92 Y and the EQU key gives 59.03 Y.

	(AR C MO – AR fc) – HD* VE x Temp HC MO	(AR * VE – AR fc) – HDC MO x Temp H* VE
Al-Battani, adapted from Nallino, Opus astronomicum, pp, 315-317	* VE [S W]	C MO [S W]
ar signif	286,60	341,42
meridian : * VE [IC | C MO [IC]	89,16	89,16
1	17,44	72,26
Dec	-21,18	-5,28
dAR	-17,94	-4,21
hd prom	4,60	0,97
temp H signif	17,99	15,70
arc	-65,34	57,03

With Placidus method, the direct arc is 57.03 Y.
----------------------------------------------------------------------------------------------------------------------

Hd prom=6.MD prom/SA prom	Hd sign=6.MD sign/SA sign
4,60	0,97
Temp H prom = (90-dAR prom)	Temp H sign = (90-dAR sign)
17,99	15,70
pm
14,54	69,03
domitude placidus = (1+dm/sa)*90	domitude placidus = (1+dm/sa)*90
104,54	159,03

----------------------------------------------------------------------------------------------------------------------

DIRECTIO CONVERSA ECHO (m) ∆ ☽ ☌ ♀

It is a converse direction as VE enters into conjunction with the trine of MO.

----------------------------------------------------------------------------------------------------------------------

speculum	Lat	Dec	AR	MD	SA	HA
VE	1,42 N	6,84 N	167,67	101,49 N	84,52 N	-16,97 E
∆MO	2,42 N	-9,86 S	210,47	58,7 N	97,94 N	39,24 E

----------------------------------------------------------------------------------------------------------------------

– MD = meridian distance (from MC if SA f [VE]  is diurnal or IC if Sa f  is nocturnal)
– SA = semi-arc (if f is diurnal, SA f [VE] is D and all MD’s and SA’s are D, otherwise N
– HA = horizontal distance (from the nearest horizon W or E for f [VE] and m ∆MO)
under bracket [] the fixed point, (here VE)
----------------------------------------------------------------------------------------------------------------------

DP REGIOMONTANUS			DP REGIO-CAMPA C		DP REGIO-CAMPA D
	A2 ∆MO	A1 VE	A1 VE	A2 ∆MO	A2 ∆MO	A1 VE
Tan A	tan dec/cos dm		31,05		-18,50
B (1)	+LG-A or -LG+A		7,43		19,98
Tan C	cot DM.cos B/cos A		13,24		31,07
Sin pole (2)	Cos C.sin LG		37,28		-32,21
Sin DA (3)	Tan pole A1.Tan Dec A2 Tan pole A2. Tan Dec A1	DAP	5,24	-7,60	6,29	-4,33
AO (4)	AO ± DA		162,43	218,07	216,75	163,34
arc	AO1 – AO2			-55,64		-53,41
				CONVERS		DIRECT

----------------------------------------------------------------------------------------------------------------------

(1) B must be < ε
(2) sign of pole has the same sens of LG for DA. Here, DA = DAP
(3) [+] sign if pole A and Dec have the  same sign; sign [-] if pole and Dec have the opposite sign
(4) to find AO of a star A2 under the pole of A1, we calculate the  DA of A2 under the pole A1 ex: tan pôleA1.tan DecA2=sin DA A2/poleA1

the converse arc is 55.64 Y.

Explication :
----------------------------------------------------------------------------------------------------------------------

----------------------------------------------------------------------------------------------------------------------
VE progressed longitude is 213.75° and TRI MO radix is 211.79°. So the diff is -1.96° and that corresponds to an arc of 55.64 Y (key EQU : 56.86 Y so diff : 56.86-57.77 <2°). 57.77=1568.68 (birth) - 1626.45 (even). Don't forget that it is a true directio conversa.

-----------------------------------------------------------------------------------------------------

DP PLACIDUS	Plac direct	Plac conv
sa1/dm1	1,67	1,22
sa2	84,52	82,06
x	50,66	67,48
dm²	101,49	121,30
sign	-1	-1
-------------------------------------------------------------------
arc	50,83	53,82
-------------------------------------------------------------------
FOMALHAUT-CHOISNARD
X = sa2.dm1/sa1
sign : if the two points are on either side of the meridian, take +1 ; otherwise -1
Arc = dm2 ±sign.x

-------------------------------------------------------------------------------------------------------

On July 8, 1626, the philosopher exchanged his prison in Naples for that of the Inquisition in Rome. It is true that from July or August 1628, he was authorized to live in the palace of the Holy Office “loco carceris”. — But it was not until April 6, 1629 that he was definitively pardoned and left in complete freedom. To this was limited the alleged benevolence of Urban VIII towards him, painfully won by Campanella after his arrival in Rome, and moreover, as we will see, quickly lost.

DIRECTION APRIL 1629

We find a (m) [c] conj MO TRI VE but the orb is at 2.36°.

New accusation against Campanella in 1634 : In 1634, an event of real gravity suddenly set things on fire. In April, the viceroy of Naples, Monterey, charged Campanella and his family with participation in a plot attempted against the Spanish authorities of that city by one of his disciples: Tommaso Pignatelli. e cette ville par un de ses disciples : Tommaso Pignatelli,  and he tried to obtain his extradition from the Vatican. His request was not accepted, and Pignatelli, who had previously denounced his master, retracted before dying. However, Campanella understands that the provisions of the Secretary of State towards him are only half reassuring, and fearing new prosecutions from the Spaniards who persist in accusing him, he takes refuge with the French ambassador, Count de Noailles.


We then find two directions: [c] conj JU square MA and # VE conj JU. The first of these directions is converse and once again involves MA.


DIRECTIO CONVERSA : [c] ☌ ♃ ☐ ♂

speculum	Lat	Dec	AR	MD	SA	HA
JU	0,48 N	-20,47 S	241,75	26,41 N	107,26 N	80,85 E
□MA	0 S	-18,22 S	310,79	42,63 N	105,17 N	62,54 W

– MD = meridian distance (from MC if SA f [JU]  is diurnal or IC if Sa f  is nocturnal)
– SA = semi-arc (if f is diurnal, SA f [JU] is D and all MD’s and SA’s are D, otherwise N
– HA = horizontal distance (from the nearest horizon W or E for f [JU] and m □MA)
under bracket [] the fixed point, (here JU)
----------------------------------------------------------------------------------------------------------------------

DP REGIOMONTANUS			DP REGIO-CAMPA C		DP REGIO-CAMPA D
	A2 □MA	A1 JU	A1 JU	A2 □MA	A2 □MA	A1 JU
Tan A	tan dec/cos dm		-22,62		-24,10
B (1)	+LG-A or -LG+A		15,86		14,38
Tan C	cot DM.cos B/cos A		-64,52		49,06
Sin pole (2)	Cos C.sin LG		-15,53		-24,06
Sin DA (3)	Tan pole A1.Tan Dec A2 Tan pole A2. Tan Dec A1	DAP	5,95	5,25	8,45	9,60
AO (4)	AO ± DA		247,71	316,04	302,34	232,16
arc	AO1 – AO2			-68,33		70,18
				CONVERS		DIRECT

(1) B must be < ε
(2) sign of pole has the same sens of LG for DA Here, DA = DA/pole A
(3) [+] sign if pole A and Dec have the  same sign; sign [-] if pole and Dec have the opposite sign
(4) to find AO of a star A2 under the pole of A1, we calculate the  DA of A2 under the pole A1 ex: tan pôleA1.tan DecA2=sin DA A2/poleA1
----------------------------------------------------------------------------------------------------------------------

the arc is convers : -68.33 Y (true converse direction).

directio conversa	(AR C JU – AR fc) – HD□ MA x Temp HC JU	(AR □ MA – AR fc) – HDC JU x Temp H□ MA
-1
Al-Battani, adapted from Nallino, Opus astronomicum, pp, 315-317	□ MA [S W]	C JU [S E]
ar signif	310,79	241,75
meridian : □ MA [IC | C JU [IC]	88,16	88,16
1	42,63	153,59
Dec	-18,22	-20,47
dAR	-15,17	-17,26
hd prom	1,48	2,43
temp H signif	17,53	17,88
arc	68,52	-69,89

----------------------------------------------------------------------------------------------------------------------

Hd prom=6.MD prom/SA prom	Hd sign=6.MD sign/SA sign
1,48	2,43
Temp H prom = (90-dAR prom)	Temp H sign = (90-dAR sign)
17,53	17,88
pm placidus
36,48	22,16
domitude placidus
126,48	67,84

----------------------------------------------------------------------------------------------------------------------
The placidus arc is : 68.52 Y. (the Placidus key provides a value of 70.7 Y).

'The kind words of Louis XIII, the kind welcome of Richelieu, who consulted the king on Italian affairs, the liberalism of the Sorbonne towards him and the reputation acquired among the lords of the Court and scholars are for him probably so many signs of the times, and confirm in his mind the astrological forecasts according to which the eldest daughter of the Church is ready, according to her request, to take in hand the great cause of religious unity and theocracy universal. This hope, expressed many times in the dedications of his works to Chancellor Séguier, to the superintendent of finances Bullion, to Louis XIII, and especially to Cardinal Richelieu, to whom he proposed to found the City of the Sun, became for Campanella a certainty after the birth of the dauphin, the future Louis XIV, from whom he himself draws the horoscope. The day this prodigious event occurred, unexpected by everyone, but announced by astrology The horoscope is not flattering; in some ways it is prophetic. Campanella pulled him out after examining the young dolphin naked, twice. He had been called to the Palace by Richelieu, at the request of Anne of Austria who wanted to know the future of her son (Amabile, Cast., t. II, p. 132-136). He would have said: “Erit puer ille luxuriosus, sicut Henricus quartus, et valde superbus. Regnabit diu, sed dur, tamen congratulate; desinet misery and in fine erit confusio magna in Religione et in Imperio”. This horoscope was copied by Barrière (Unpublished Memoirs of Louis Henry de Loménie, Count of Brienne, 2 vols., Paris, 1828, vol. I, p. 346, note c), on a print from 1638, preserved in the Library National in Paris (Cabinet des Estampes, volume for the year 1638-1639). — Previously the philosopher would have foreseen the unexpected birth of Louis XIV, which he calls a “portentosam nativitatem”: “In France he performed several acts as an astrologer; consulted by Cardinal Richelieu if Monsieur would ascend the throne, he replied: Imperium non gustabit in aeternum”. ' (Naudaeana, Paris, Florentin and Delaulne, 1701, p. 4 and b). [Campanella à Rome et à Paris, pp. 63-64, Léon Blanchet, 1920, Alcan]