URBANUS VII (2) - Soli Lunar phase (4)
Pope Urban VII (4 August 1521 – 27 September 1590), born Giovanni Battista Castagna, was head of the Catholic Church, and ruler of the Papal States from 15 to 27 September 1590. His papacy was the shortest recognized in history. Giovanni Battista Castagna was born in Rome and died in Rome on 27 September 1590 of malaria. He had reigned for 13 days and died before he could be crowned. He was buried at St. Peter's Basilica.
See also https://primarydirections.blogspot.com/2017/09/argoli-3.html
Argoli only explores directions touching the MC or the ASC; in the case of Urbaus, he shows that around the age of 69, we find ASC ◻ ♄ and MC ☌ ☉. If we compute the data, we find :
- OA ASC 163.53°
- OA ◻ ♄ (Z) 232.88°
-------------------------------
- diff 3.04
Interested in Placidus's method (formerly known as the method of Al-Battani and Al-Biruni (see Schirmer, 1934, Encyclopedia of Islam) and fully theorized by Carlo Alfonso Nallino (Al-Battānī sive Albatenii Opus astronomicum, pp. 315-317; Nallino, Batt II, pp. 283-289 and I, pp. 131-134 III, 200-202), we studied the Primum mobile... published in 1657 and developed a process for writing a commentary on a direction under study "as if" Placidus was writing. A reference table is attached to it to track the parameters while reading.
If we now return to Argoli, we notice that while he focused on the study of axes, he completely neglected the interactions planetary. Let us therefore see in the case of Urbanus VII, what occurs in his birth chart on the date corresponding to September 27, 1590 (i.e. 150.74 or 69.15 in age).
The converse direction ◻ ☽ ☌ ♂ is found around 71.78 years (key EQU, 1.038).

In our research, we hypothesised that the mundane chart alone should be considered; also we must base on the aspects taken in the semiarcs the research of the degrees likely to be considered in the duration of the life.
In the case of Urbanus VII we have the table above which allows us to estimate the breakdown of aspects between the different planets and the alchocoden.
When considering a theme, the first thing is to observe whether it is diurnal or nocturnal. In the case of Urbanus VII, it is DIURNAL.
In this case, the first point to check is SU. If SU is well disposed, it can claim 1st stage to be HYLEG.
SU is Ru and therefore seems strong, with a dignity score of [13],
Moreover, when we look for the dignities that appear in the zodiacal inscription of SU, we find at least one
we find at least one aspect to match with the dignities
We'll see later what we get when we search for mundane dignities.
So : the hyleg is SU as dignity is Ru and aspect is conjunction
We note that SU is hyleg; it cannot be alchocoden because VE is in ☌ with it and moreover retrograde. VE does not exercise dignity over SU but the SU is itself in a condition of dignity (Ru). We are therefore in complete contradiction since there is inconsistency in the value of the link between SU and VE. This inconsistency is reinforced by a mundane ∆ (radix) aspect between JU and VE.
Now we must look for the alchocoden: it is the planet which has the maximum dignity with regard to the hyleg and which exchanges a Ptolemaic aspect with the hyleg.
if we consider the MUNDANE system, we observe a conjunction aspect of SU.
At the same time, it appears that SU has dignity of RUL over ASC.
So we have two possibilities with our hypothesis : first choose SU for hyleg ; second choose the MUNDANE system and try to find another couple of hyleg/alchocoden,
If we choose now SU we must know that no trad authority agree with this choice
In case of SU is the Hyleg, there is then one candidate to be the alchocoden: SU
First, we have to see which candidate has the most dignity: here, SU has candidate alcho dignities referring to SU : [RUL]
First, SU is linked with SU by a [conjunction] aspect and a [RUL] dignity,
However, SU is [Ru] and has a power of [13], and so SU has a good Kadkhudah score of [1]
SU is located at 140,62° at more than 5° from [Δ degrees cups sup [XI] : 28,03° (300)] and has a domitude Regio of : [328,03] for a latitude of [0°]
Now, we have to take account of the radix zodiacal aspects,
------------------------------------------------------
VE 0 SU: -6 minus alcho dy (1,97)
------------------------------------------------------
Without any change, we find with SU as Kadhkhudah : Y = 38,7 as a result of SU SUCCEDENT years
But as SU is Ru, following William Lilly in Christian astrology, p, 115 (London, 1647) on his table of Fortitudes and debilities, we remove 1/5 of his value, as dignity for SU is Ru Or (ie 0)
------------------------------------------------------
So, zodiacal Y =63,68
------------------------------------------------------
MUNDANE
Now we have to think about the hyleg to find: MO is not suitable; the rule is then in a nocturnal theme to reconsider first the case of SU,
In the mundane theme with domification, we find a RUL :SU with a conjunction for SU
SU is in ruler
So the Y are in principle : 69
But, according to MONTULMO, the alchocoden (SU) is in XI house and has two dignities in this house ; so IX is cad and not cadBut, according to MONTULMO, if the alchocoden (VE) is in IX house and has two dignities in this house ; so IX is not is not considered as cadent but as succedent. It also appears more logical that house IX, adjoining the MC and hylegial, has a standard score at least equal to 2/3 of the succedent score.
So the actual Y is 69,
To do this, the procedure is not unequivocal but one of the most logical seems to me to be the one mentioned by Auger Ferrier in ‘Jugements astronomiques sur les nativités’, Rouen, 1583 (pp, 39-51 and notably pp, 43-48). Note that Auger Ferrier's comments appear directly related to those of Montulmo in his’ De Nativitatum liber praeclarisimus’ (Nuremberg, 1540), cap IV & VII. Book translated by Robert Hand (‘On the Judgment of Nativities’, part 1 & 2, Project Hindsight, vol X)
the years of life are identified for the [succ] and [cad] houses relative to the alchocoden
In September 1590, Giovanni Battista Castagna was elected pope under the name Urbanus VII. This moment is marked to within 3° by a conjunction between MC and {☉, ♀}. Besides this conjunction, there is a sextile between MC and ♃ (noted to by Argoli) and an ☍ between ♃ and {☉, ♀} (note that the opposition of ♃ is in principle beneficial, especially since a radix aspect in trine is there and ♃ is Ru).
15 days later, Urbanus VII died from possible malaria.
I have already mentioned the squaring of AS and SA (noted by Argoli). Let us return to this converse direction ◻ ☽ ☌ ♂.
|
|
natal hour TU |
SIGNIF |
PROM |
progress hour |
| Urbanus VII |
4 8 1521 |
6h 36' 4" |
□ MO |
MA |
2h 41' 45" TU |
|
|
|
cuspal dist point |
|
|
| PLACIDUS |
CUSPAL DIST |
(*) |
□ MO |
MA |
PLAC DIR – POLE |
| directio conversa |
OA ASC |
163,53 |
signif |
promissor |
□ MO [E] | MA [E] |
| -1 |
OA □ MO |
262,36 |
OA |
OD |
asc or desc |
|
dist horiz |
98,83 |
4 |
4 |
□ MO under earth |
MA under earth |
|
house □ MO |
3 |
□ MO [MA 92,63 N] |
|
|
|
horary time (ht = 1/6 SA) |
18,23 |
109,38 |
90 |
pole Placidus □ MO |
|
double ht (1/3 SA) |
36,46 |
10,55 |
8,68 |
5,04 |
| houses |
|
22,97 |
DM |
PM |
|
| 3 |
0,33 |
7,66 |
-98,83 |
|
|
| 4 |
0,00 |
0,00 |
|
DA MA / □ MO |
OA MA / □ MO |
|
pole 3 |
17,03 |
17,03 |
-13,72 |
256,70 |
|
dec □ MO |
-20,30 |
|
|
OD MA |
|
DA □ MO /3 |
-6,50 |
-6,50 |
-1,88 |
189,22 |
|
RA □ MO |
242,98 |
|
16,20 |
67,48 |
|
OA |
236,47 |
249,48 |
|
dir |
|
dist □ MO cusp / 3 |
25,88 |
10,58 |
36,46 |
|
Comment 'from Placidus' :
The direction of the MA in the locus of □ MO by converse motion is calculated as follows:
the distance of □ MO counted from the IC (Immum Coeli) is 10,55° for its right ascension (RA) is 242,98° ; the pole's elevation of the III house and the IV is 17,03°, the semi-nocturnal arc (SA N) of □ MO is 109,38° of which ⅓ (double horary time) is 36,46°, that gives for □ MO a polar elevation of ≈ 5,04°
Note that the mundane position of the □ MO is PM = 8,68 (this is the ratio of 90° to the nocturnal semi-arc of 109,38° at the meridian distance of 10,55°).
If we wanted to determine the Placidus domitude, it would be sufficient, depending on the altitude h of □ MO - the directing aspect - (actual h =-66,63), to compute : (h<0) 270-PM or (h>0) 90-PM, or in the present case dom = 81,32, or : 21,32 [ d, III ],
In any case, at this pole, the oblique ascension (OA) of the position □ MO is 189,22° (the ascensional difference DA of □ MO under the pole of MA is DA = -1,88°) and that of the MA at this same place is OD [MA] = 256,7 ° with its own declination ; by subtraction we obtain the arc of direction |67,48|°,
This table shows a Placidus direction programmed some 'old-fashioned' with the distance of □ MO from the cusp of 3 (7,66), the width of 3 (36,46) established by double HT. We then find the DEC (-20,3), the DA of □ MO under the pole of cusp 3 3, RA and OA of □ MO. We then calculate the PM of □ MO (8,68)
Regio comment
The direction of □MO in the place of MA by converse motion is calculated as follows :
First of all, it must be considered that the so-called immobile positions of the theme are the significators: these positions (and their aspects on the ecliptic) are driven by the movement of the primum mobile and are called promissors. There is an ambiguity here that we have repeatedly raised: if we draw up a horoscope within 2 hours (let's say) following birth and according to what we have just stated, we observe that it is the significator that "seems" to have moved while the promissor "seems" to have remained immobile. We must never forget this ambivalent feeling when practicing the art of direction.
It should now be noted that the circle of position of a star is strictly the same in the Campanus and Regiomontanus houses (as Max Duval pointed out (in ‘la domification et les transits’, p, 33, Ed Traditionnelles, 1984)) and that only the "registration numbers" of the domitudes change (they are not expressed in degrees: Christophe Vitu has noted (http://mapage.noos.fr/astrolabe/latitude.htm#Domitude):
"It is by abuse of language that we note the domicile in degrees, because this only really represents a measurable angle for a star located on the equator, in this case the diurnal arc is worth 180° (12 hours), and the domitude then corresponds to a sort of hourly angle which would be measured in the direct direction from the East point. In all other cases the domicile cannot be assimilated to an angle, its values go from 0 to 180 for nocturnal houses and from 180 to 360 for diurnal houses, the culmination being identified by the value 270, each house worth 30."
The domitudes are linked by the relationship:
tan d Regio = tan d Campa/cos ⅄,
Henri Selva (‘La domification ou construction du thème céleste en astrologie’, Vigot ed., 1917, réed Lacour/Rediviva, 1992, p, 15) noted that Campanus' method is quite similar... to the 'rational method' (Regiomontanus)
---------------------------------------------------------------------------------------------------------------------------
| speculum |
Lat |
Dec |
AR |
MD |
SA |
HA |
| MA |
0,23 N |
-2,92 S |
187,34 |
66,19 N |
92,63 N |
26,44 E |
| □MO |
-0,87 S |
-20,3 S |
242,98 |
10,55 N |
109,38 N |
98,83 E |
| DP REGIOMONTANUS (5) |
|
|
4 |
quadrant |
4 |
|
|
|
h |
-19,52 |
|
-66,63 |
|
|
|
dec |
-2,92 |
|
-20,30 |
|
|
|
|
DP REGIO-CAMPA D |
|
DP REGIO-CAMPA C |
|
|
A2 □MO |
A1 MA |
A1 MA |
A2 □MO |
A2 □MO |
A1 MA |
| Tan A |
tan dec/cos dm |
|
-7,20 |
|
-20,62 |
|
| B (1) |
+LG-A or -LG+A |
41,9 |
34,70 |
|
21,28 |
|
| Tan C |
cot DM.cos B/cos A |
|
-20,09 |
|
79,41 |
|
| Sin pole (2) |
Cos C.sin LG |
|
38,84 |
|
7,05 |
|
| Sin DA (3) |
Tan pole A1.Tan Dec A2
Tan pole A2. Tan Dec A1 |
DAP (6) |
-2,35 |
-17,33 |
-2,62 |
-0,36 |
| AO (4) |
AR ± DA |
|
189,69 |
260,31 |
245,60 |
187,70 |
| Arc (7) |
AO1 – AO2 |
|
|
-70,62 |
|
57,90 |
|
|
|
|
DIRECT |
|
CONVERS |
(1) B must be treated as positive number (< LG)
(2) sign of pole has the same sens of LG for DA Here, DA = DA/pole A
(3) sign [-] if pole and Dec have the opposite sign ; sign [+] if planet located in western half, sign [-] if planet located in eastern half ; Signs [+] and [-] must be reversed for births in the southern hemisphere
(4) to find AO of a star A2 under the pole of A1, we calculate the DA of A2 under the pole A1 ex: tan pôleA1.tan DecA2=sin DA A2/poleA1
(5) algorithm and lessons from : a)- Gouchon (‘Dictionnaire astrologique’, Dervy, 1946, 1975, p, 276, attributed to H. Selva) ; b)- Martin Gansten (‘Primary directions’, pp, 155-157, 2009, Wessex Astrologer) - instructions for use only appear in Gansten – c)- Astrologia gallica, Morin de Villefranche, trad Holden (appendix 5, pp, 151-153) ; d)- Henry Coley, Clavis astrologiae elimata, 1676, pp. 609-648 ; e)- Henri Selva, La domification, Vigot, 1917, reprint Lacour 1992, p, 25 and 131
(6) ascensional difference under own pole
(7) if the 0° point of the equator (viz 0° trop ARI) should fall between one of the two points, 360° must be added to arc
---------------------------------------------------------------------------------------------------------------------------
Here we find arc = -70.62 Y.
Luni-Solar Phase

This is a method that we find outlined in Vettius Valens [book VI 9] as indicated by Anthony Louis in his blog :
'Vettius Valens had a different notion of annual returns. He felt that the return of the Sun each year was insufficient for forecasting for the year ahead because it omitted the influence of the the Sun’s partner, the Moon. As a result, Valens used a hybrid chart for the annual return which consisted of the positions of the planets when the Sun returned to its natal position each year but these positions were placed in a chart whose Ascendant and houses were determined by the moment the Moon returned to its natal degree during the zodiacal month when the Sun was in its birth sign.' [The Tithi Pravesh and its Monthly and Daily Iterations, November 5, 2022]
Placidus uses it in his Primum mobile (Tabulae primi mobilis cum thesibus et canonibus 1657) and gives the procedure to follow in the XL canon (De Progressionibus, p. 53). A complete example appears in the analysis of the theme of Charles V (Exemplum Primum Caroli V. Austriaci Imperatoris, pp. 59-62).
There is only one site on the internet that does this calculation: https://horoscopes.astro-seek.com/calculate-planet-revolutions-returns/
but it only gives the soli-lunar return at D0; Placidus continues the progression until end of process (i.e. even). For example in the case of Urbanus VII, if we take the date of 27 Sep 1590, we must first translate this date into 'life-year equivalent': we find :
---------------------------------------
EVEN 69,1500070756704 69 Y
0 1,80008490804414 1 M
24,0025472413242 24 D
0,0611337917816854 0 H
3,67 M
---------------------------------------
The method of “embolismic lunations” as a predictive technique : See : Tabulae Primi Mobilis,,, Placido De Titis, Patavii, MDCLVII
An embolismic lunation, correctly termed an embolismic month, is an intercalary month, inserted in some calendars, such as the Jewish, when the 11-days' annual excess over twelve lunar months adds up to 30. An arbitrary application of this was used by Placidus, who applied the term Embolismic Lunation, to a Figure cast for the moment of the Moon's return to the same relation to the Sun that it occupied at birth. It was made the basis for judgment concerning the affairs and conditions of the ensuing year of life.' [https://astrologysoftware.com/community/learn/dictionary/lunation.html]
The solar year does not have a whole number of lunar months (it is about 365/29.5 = 12.37 lunations), so a lunisolar calendar must have a variable number of months in a year. Regular years have 12 months, but embolismic years insert a 13th "intercalary" or "leap" month or "embolismic" month every second or third year [...]. Whether to insert an intercalary month in a given year may be determined using regular cycles such as the 19-year Metonic cycle [...] or using calculations of lunar phases [...]. [wikipedia]
The whole difficulty therefore comes from the fact that there is no overlap between the solar month (30 D) and the lunar month (synodic month 29.53), consequently between the solar year (365.242) and the lunar year (354.367).
'In Vedic timekeeping, a tithi is a "duration of two faces of moon that is observed from earth", known as milа̄lyа̄ [...] in Nepal Bhasa, or the time it takes for the longitudinal angle between the Moon and the Sun to increase by 12°. In other words, a tithi is a time duration between the consecutive epochs that correspond to when the longitudinal angle between the Sun and the Moon is an integer multiple of 12°. Tithis begin at varying times of day and vary in duration approximately from 19 to 26 hours. Every day of a lunar month is called tithi.' [wikipedia]
We see that the interest of Placidus' method (outlined by Vettius Valens) comes from the fact that the individualisation structure of the progression system is no longer represented by a single point (solar return or lunar return) but by a distance ( in this case the distance between SU radix and MO radix).
We find in the literature another method which is similar to that of the solilunar phase: it is the tertiary directions. We find a critique of it in “Les Moyens de pronostic en Astrologie” by Max DUVAL [ed Traditionnelles, 1986, pp. 67-71] and a complete analysis in "A close look at tertiary progressions" by Elva Howson & Jack Nichols, [Considerations, vol XI-4, 1996; pp 3-12]- https://archive.org/details/considerations-21-1/considerations-11-4/page/n1/mode/2up
In the case of Urbanus VII, we observe:
SU radix = 327° 25' 18" (327,42° AQU)
MO radix = 43° 28' 57"° (43,48° TAU)
∆ = |283° 56' 20"| (283,94° ) [ 23 tithi = ROUNDUP (∆/12)]
Here is now the way in which Placidus would have proceeded: for 60 full years, 55 embolismic lunations are accomplished in 9 years after birth but with 33 days less, that is to say 11*5 since the moon covers 12 lunations in 11 days less than a whole year, as indicated in canon XL
... if you wish to have a ready calculation of the progressions for several years, note that the moon does not complete twelve lunations in one whole year -i.e. a solar year - but in eleven days less. Having therefore the distance from the moon to the sun in the sky of birth, search for this eleventh day before the end of the first year of life and having found it, then know that the progression of twelve years of life is completed. Likewise 22 days before the end of the second year after birth gives the progressions accomplished for 24 years and so on' [De Progressionibus, op. cit., p. 54]
Therefore on 3 AUG 1526, by removing 55 days, we arrive at 10 June 1526 [,,,] and then, the process is completed for 55 full years. Then, for the 9 other years elapsed during the twelve embolismic lunations, I arrive at 26 February 1527, for the remaining 8 months and 21 days. I compute the tithi (exact distance between SU and MO radix) for the last time : the date of Embolismic Progression J0 is : 2 February 1527 at 15h 11min tu. Thereafter, i add to this date 4,43 d corresponding to 1,8M [see EVEN] :
JD Pr Emb = 1,8 x 30 / (365.24 /29.53) = 4,43 D
where 365.24 is the number of tropical days in a year and 29.53 is the average period for the synodic month of MO
trop days 365,242219061458 (1)
syn month = 29,5305878104754 (2)
where T = (JD-2451545)/36525
In the present case JD = 2278831,5
so, T = -4,78375085557837 (see formula 1 and 2)
Finally, we find : date for J4,43D = 7 February 1527 at 1h 29min local (1h 30min TU).
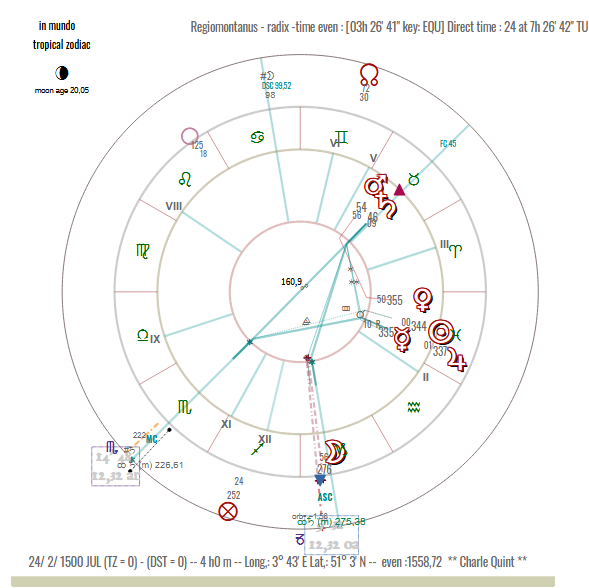
At this stage, we find the aspect :
♂ ◻ {☉, ♀
} which is perfectly in agreement with what we wrote above. It is likely that Giovanni Battista Castagna was ill before his election, in which case the soli-lunar phase would have to be postponed to D0 of the current cycle:
Using the same process, we find the date of 2/2 1527 at 16:0 p.m. UT for J0. The aspects are more important: we find the ♂ ◻ {☉, ♀
}, we add to it ♀
☌ ♄ and an echo direction ☽ ◻ ♃ et ♃ ◻ ☽.